Instant Gravity Proof
 
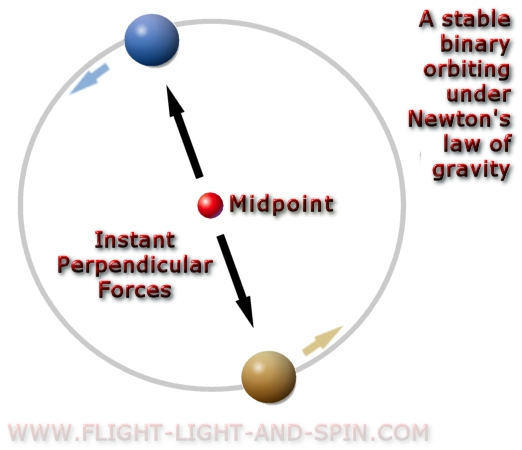
All the geometry within this article evolved in computer algorithm. The software used is orbit-gravity-sim-11.exe which is free to download. The program demonstrates the evolution of binary-orbits in real-time under a variety of gravity theories.

Consider a pair of equal-mass binary stars. Ponder how the velocity of gravity will affect the shape of these orbits. First consider gravity to be instant as Newton theorized; then consider it to travel at the velocity of light as Einstein proposed. Surely it is crystal clear that these two different theories will not yield the same result?
.
  
     
 
 
   
     
 
If gravity travels instantly then it must pull at an angle precisely perpendicular to the orbit-line directly across the midpoint. But if gravity travels at the velocity of light then it would pull to the position where the opposing star was when the gravity departed from that star. The gravity must first travel the distance between them before it can pull on the opposing body. This will affect the shape of the binary orbit.
.
  
     
 
 
   
     
 
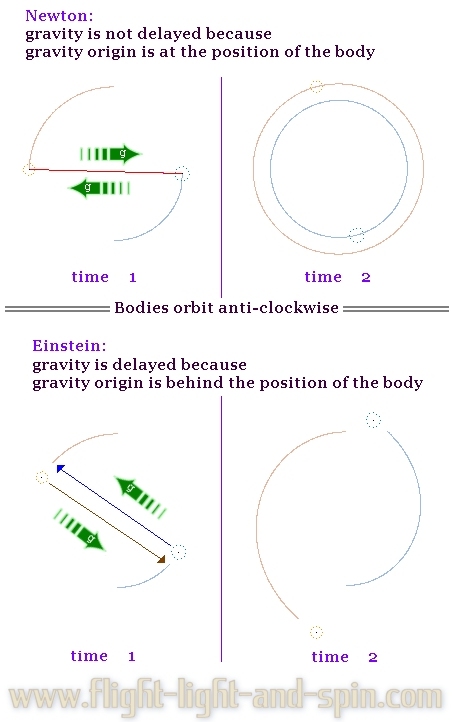
If gravity travels at the velocity of light then binary star-systems will spiral outwards away from each other. Because most stars form binary pairs, gravity must be propagated instantly in order to ensure that binary orbits persist for many billions of years as they are commonly observed to do. The rate of outwards spiral depends on their velocity and distance apart.

The binary pair in the next graphic have slightly different mass to each other. They evolved strictly under algorithm orbit-gravity-sim-11.exe. This clearly shows that if gravity travels at the velocity of light then the force must pull to a point away from the midpoint (barycenter) of the binary pair.
.
  
     
 
 
  gravity instant proof  
     
 
Note the gap between the orbit-line and the body. This designates that the origin of the force of gravity is not the same as the position of the body.

However, the famous LIGO experiments postulate that a binary pair supposedly spiral inwards if gravity moves at the velocity of light. So let us use more detail so that we can establish by how much a binary pair would spiral outwards if gravity travels at the velocity of light.

At about 2500km apart, a binary pair of equal mass (both 33 solar masses) with an almost circular orbital-shape travels at roughly one-tenth the velocity of light. So the delay in gravity causes a divergence between the gravity origin and the body itself of about one-tenth the distance between them. There is thus a gap of about 250 km between where the body actually is and where it was when it generated the gravity that eventually reaches the opposing body.

Because the bodies travel at 1/10th the velocity of light, the gap between the body and the gravity origin is about 1/10 of the distance between the pair of bodies.

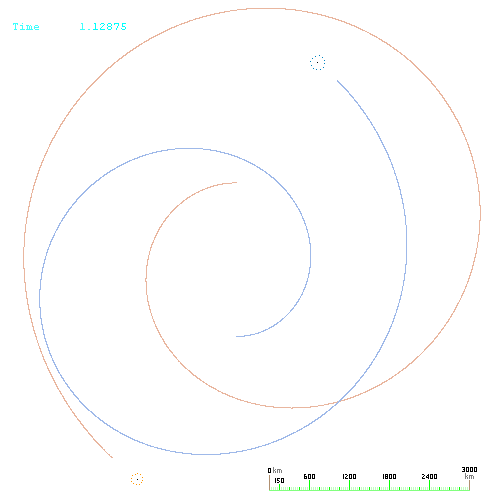
That is a very big gap, proportionally speaking. So we can see what this looks like with more accurate information. These graphs evolved in orbit-gravity-sim-11.exe with gravity moving at the velocity of light with data similar to the famous LIGO binary pair GW150914.
.

  
     
 
 
  proof of instant gravity  
     
 

The binary pair spiral outwards so rapidly, that it is easy to see how they could never have started out that close together in the first place. It would not be possible for a pair of 'black-holes' to reach an orbit as close as 2000km apart as the LIGO theorists suggest - if gravity travels at the velocity of light. The next graph is the same example as above but progressed further in time.
.

  
     
 
 
   
     
 

Perhaps that data is a not quite down to Earth enough for you?

Consider a binary pair of stars each 1 solar mass about the same distance apart as our Sun to the Earth. We know that it would take about 8 minutes to travel that distance at the velocity of light. A roughly circular orbit this distance from the Sun needs to move at about 21 km per second. So there would be a divergence in this example of an amount which is 500 secs x 21 km/s. A disputed gap of over 10000 km in the direction that gravity is pulling this binary pair is certainly a significant amount.

Now when the binary pair are in a highly eccentric orbit, the outwards spiral increases due to the velocity of the pair increasing when they are closest together. So in the next example consider binary stars similar to the Alpha Centauri pair of roughly 1 solar mass each with quite an eccentric orbital shape.

However, in this example we start them very close together. Under Newtonian laws their maximum distance apart is well within the orbit of Mercury. After just 20 000 orbits the maximum distance between the pair would be way beyond the orbit of Pluto - if gravity moves at the velocity of light.
.

  
     
 
 
  instant gravity proof  
     
 

After 20 000 orbits the binary pair of one solar mass each would be spiralling away from each other by more than a million km per orbit - if gravity travels at the velocity of light. And that amount would be increasing by well over 50km for every orbit. This concept has been termed BOGVOS: Binary-Orbit, Gravity-Velocity, Out-Spiral.

This article is a brief summary of my full analysis of the concept of gravitational-waves as proposed by the LIGO group within the context of the GW150914 experiment. All the graphs are demonstrated with the scale set at a few thousand km. The distances beyond that are progressed estimates based on this scale. The downloadable gravity simulator orbit-gravity-sim-11.exe (OGS11) that generated these graphics is freely available at this link: download OGS11

The full analysis here: Analysis-GW150914-Bain.pdf is 37 pages, 4mb.

A shorter 10-page summary is here: Anaylsis GW150914

Jonathan Ainsley Bain
South Africa, 2017 AD
.

  
     

 

 

 

Instant Gravity

The quickest mind always entertains every logical possibility.

^ top of page ^