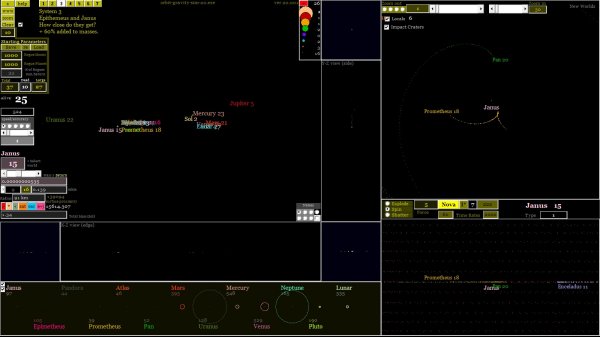
The
object of this gravity simulation started out purely to demonstrate
the delicacy of Saturn's curious rings and moons, generally.
But then I discovered the incredible nature of the orbits of
Epimetheus and Janus. They have a very tricky orbital dynamic
to describe with words, the easiest explanation being that they
form a horseshoe orbit. Their orbits are so close to
each other that the two moons actually switch orbits instead
of colliding.
The masses of the moons cause their own gravity dynamic to behave
thus, and if they had much less mass, they would not perform
this celestial dance. But there was some discrepency as to how
close they get to each other. Their orbital distance from Saturn
differs by only 50 km.
That is the distance from each of these two moons, to Saturn,
differs by only 50 km. But they are both well
over 50 km in size!
However, they never get closer than either 10
thousand or 15 thousand km, due to their own
gravitational forces affecting one another.
This sounded absurd, So I redirected this algorithm away from
trying to figure out the dynamics of Saturns rings, and instead
focussed it on this pair of curious moons.
It was a joy to see the orbits behave in my Newtonian-Planck
evolutionary algorithm, just as observed. The only noticeable
difference was that discrepency of:
10 000 km or 15 000 km before
they switch orbital places.
What I was able to prove was that with given masses:
1.98 x 10^18 kg ... Janus
5.5 x 10^17 kg ... Epimetheus
the pair came within 10668 km of each other:
[Scenario 2],
but if I add 60% mass to each of them,
then they were within 15614 km of each other:
[Scenario 3].