To download orbit-gravity-sim-11.exe visit here: OGS11 download page.
The full pdf article has a more detailed explanation of the following summary.

The user can get ‘tool-tips’ from the software whilst it is running, by simply hovering the mouse over the various buttons and boxes. For example: hover the mouse over the distance between the pair (‘E’) to see the exact (un-rounded) maximum and minimum distance between them. The following screenshot outlines some of the features of the software, with a few explanations:
.

Use the ‘pause’ button; then move the binary pair around the screen if you want; change the amount of gravity (mass) of each; as well as alter the momentum. This demonstrates that the model is dynamically accurate to conventional physics properties, and is not just a video simulation.

Physical Cosmology:
Label ‘A’ points to the most vital feature. The frame on the top right of the screen allows various physical laws to be ticked on/off and variables altered. Each scenario uses these differently, but you can also alter them whilst the scenario is busy evolving. It may be ideal to start the scenario; press the pause button; then alter the physics; and then un-pause. Otherwise the pair may bind before you can have time to alter the physics. But it works either way.

Before you start any of the [27] scenarios (label ‘B’ in diagram previously), you may want to click through the Physics Cosmology options, some of which give descriptions. Hovering over each of them also gives brief descriptions as ‘tool-tips’.
.

A list and summary of the various scenarios:

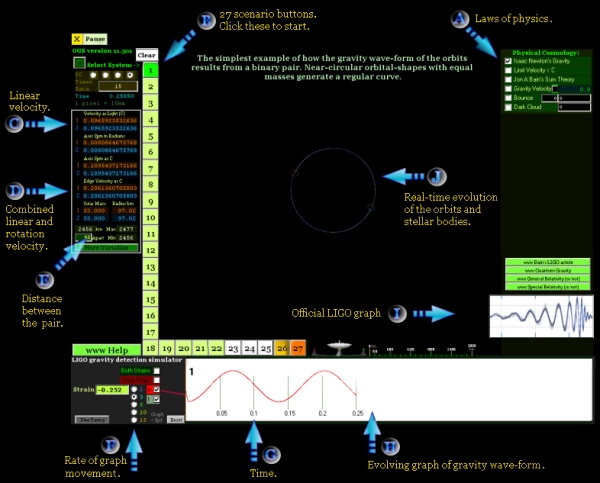
[1] The simplest example of how the gravity wave-form of the orbits results from a binary pair. Near-circular orbital-shapes with equal masses generate a regular curve.
[2] This demonstrates the problem: Binary-Orbit, Gravity-Velocity, Out-Spiral (BOGVOS).
[3] This scenario shows the LIGO wave-form estimated as the best computation within the theoretical framework from Abbott and the LIGO scientists. The expected wave-form is not the result. The limit of the velocity of light from Special Relativity causes the pair to drift back and forth once after 30 orbits. This is reflected in the observed gravity wave-form. To see the smaller wave-form of the orbits: Start the scenario; then pause it. Click ‘Fine Tuning’ and change the ‘Stiffness’ variable from 0.8 to 0.9999. Un-pause to continue the scenario.
[4] Binary pair with unequal mass and uniform orbits. There is no in-spiral or merger in a purely Newtonian paradigm. The wave-form oscillates evenly with the circular orbits in Newtonian physics even when the pair has unequal masses.
[5] Instead of in-spiral from Special Relativity, it is possible that the in-spiral could occur due to collisions with a cloud of matter. This shows that the in-spiral results in a decrease in amplitude.
[6] The gravity wave-form of the orbit with a pair of equal mass merging. With an in-spiral caused by a cloud of matter, this scenario fails to show an increase in amplitude of the wave-form due to the contact and merging process.
[7] This option is a preliminary intuition which served two purposes. Firstly it is a test case to ensure that the angle of incidence is correct when the pair collide with a glancing blow. Secondly it was an intuition that the wave-form may have occurred due to the pair enduring a series of glancing blows before they merge. This did not quite give the correct wave-form, but it was a close guess.
[8] Unequal mass and horizontal eccentric orbits according to the Newtonian paradigm.
[9] Unequal mass and vertical eccentric orbits according to the Newtonian paradigm.
[10] Vertical eccentric orbits with equal masses according to the Newtonian paradigm.
[11] Horizontal eccentric orbits with equal mass according to the Newtonian paradigm.
[12] Tests how the spin affects the orbit at collision.
[13] Newtonian scaling test. Distance of 350km yields 75Hz for combined 66 solar masses. OGS11 is in agreement with the Newtonian estimates of the LIGO group.
[14] Sum Theory demonstrates that mass is lost when the edges of the bodies approach the velocity of light. Velocity turns into spin as an object approaches the velocity of light.
[15] Observe how the limit of velocity at the velocity of light results in the in-spiral. Just the orbit-lines are here depicted (see ‘Horizon’ option). The closer to circular the orbits are, the less in-spiral occurs. Compare this scenario with scenario [4] by enabling ‘Limit Velocity < C’ in that scenario to see comparatively almost no in-spiral.
[16] If gravity propagates at the velocity of light, the pair spiral outwards. This also includes the much smaller spiral inwards from the limit on velocity from Special Relativity, as well as the in-spiral from the cloud of dark matter. The result is still an outward spiral.
[17] Gravity is at the velocity of light from General Relativity. A loss in velocity from Special Relativity tries to cause an in-spiral. Momentum is much less to try and cause an in-spiral, but they still out-spiral.
[18] With the pair starting at a large distance apart, and the in-spiral caused by a cloud of dark matter.
[19] Binary pair with unequal mass - at large distance. Gravity delay and limit as object approaches the velocity of light included (General and Special Relativity).
[20] With the pair about 600km apart and gravity propagated at 6x the velocity of light there is still no equilibrium between in-spiral and out-spiral. Decrease the velocity of gravity to increase the outwards spiral. Take special note of the ‘timer delay’. If this number gets too low (less than 3) then the computer speed causes a large rounding-off error. This can only be improved upon with a faster computer process. But it does not affect the principle of the matter.
[21] This uses the Special Relativity velocity limit for the pair at the velocity of light but now starts the algorithm with the pair over 2300km apart. Even with gravity propagated at 50 times the velocity of light, the outwards spiral is still more than the in-spiral from the limit at the velocity of light.
[22] At a distance of over 5750 km between the pair, if the velocity of gravity is about 99 times the velocity of light, there is still out-spiral. If the velocity for gravity is higher than this, the timer delay goes beyond the margin of error at this scale.
[23] A binary pair of white dwarfs; each the mass of just 1 sun. (NOT super-dense ‘black holes’). Less mass requires less velocity, the result is that they are larger and orbit more slowly than the ‘black holes’. This example is Newtonian.
[24] A binary pair of white dwarfs; each the mass of just 1 sun. With in-spiral from Special Relativity, and velocity of gravity from General Relativity the pair spiral away from each other at an ever increasing rate. They start about 2450km apart here.
[25] This is the same as the scenario [24], except that the starting momentum is less in order to try and get the pair to in-spiral. Either way, they out-spiral due to the delay in gravity.
[26] Close non-binary orbit. Observe how Einstein's limit at the velocity of light affects the shape of the eccentric orbit of the smaller body. This represents possibly the most fascinating result. This is not at all in-keeping with claims of how the orbit of Mercury is supposed to advance. Mercury should actually be spiraling into the Sun if Einstein’s limit on the velocity of light is valid. A loss in velocity must surely cause an in-spiral.
[27] Seeing as though there is no known physics that results in the energy of the system increasing both the amplitude and the frequency of the signal, and gravity must be instantaneous; the only conclusion is that the wave-form is an artificial electromagnetic construct. Read more about this vital intrigue at the end of the chapter.
.