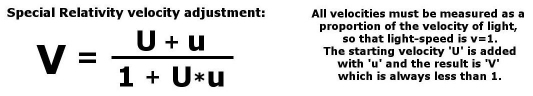| N-body Relativity The
algorithm orbit-gravity-sim-12.exe
(OGS12) must first determine the exact velocity of a star or planet,
in order to impose the principle from Special Relativity, which
decreases the Newtonian acceleration so that nothing can move at
or beyond the velocity of light. |
||
|
But any velocity can only be measured by comparing it with a starting
reference point of zero velocity. Now in Newtonian terms, the shape
of an orbit seems to be the same regardless of where we take that
starting point. Newton’s laws are thus said to produce identical
results in all reference frames. But in Einstein’s Relativity
where we take the starting reference point to be, will change matters
fundamentally; most specifically in systems of numerous bodies.
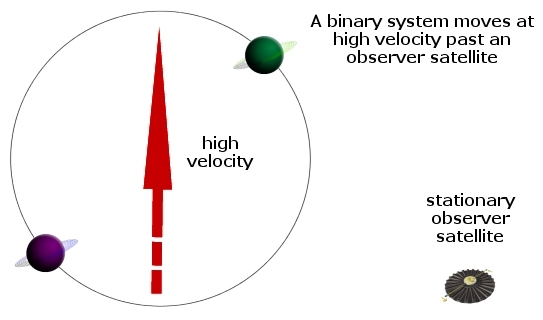
The simplest way to realize this is to envision a binary system of stars moving past an observer such that the binary system is at a high velocity compared to the observer. However, in comparison to one another, the two bodies in the binary pair are orbiting one another quite slowly. Under
Newtonian laws, the shape of the orbits in that binary system apparently
changes zero in comparison with one another or in comparison to
the observer regardless of where we take the starting reference
point to be. |
||
|
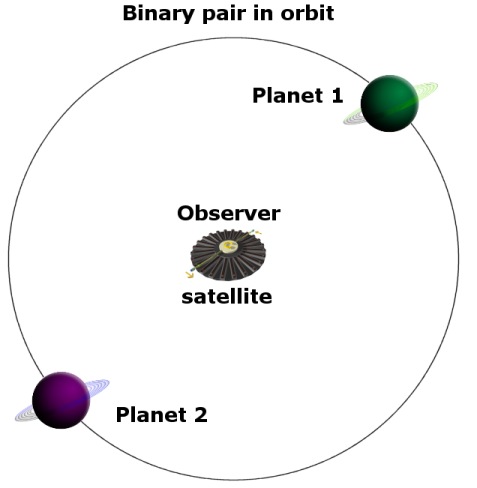
But in Relativity, if those velocities are taken from the point
of view of the midpoint (barycenter) of the binary pair they would
then not have much velocity reduction – they would not spiral
inwards by much. They have low velocity compared to one another
so they are changed little by the formula: ‘Special Relativity
velocity adjustment’ (depicted earlier).
However, from the perspective of the observer they are moving past at high velocity, their velocities would both be high and thus reduced more radically away from the Newtonian amount by Einstein’s formula. They would spiral inwards more if we observe them from the satellite they are moving past at a rapid rate, than if we observe them from the midpoint between the pair. Relativity gives us contradictory shapes to the orbits depending on their comparative velocity to the observer. This is quite contrary to the claim that Relativity is the same in all reference frames. It certainly cannot be, even though it insists it is! Now those who have not attempted to construct an algorithm with 3-bodies depicting Special Relativity may decide to disagree here. You may choose to believe that the larger velocity reduction from the perspective of the observer satellite is the same in Relative terms to the smaller reduction when comparing the pair to one another. You will also need to carefully consider the discussion on the various methods used to calculate this reduction in two dimensions in the previous chapter. So if you feel utterly certain that Special Relativity will yield the same results in all reference frames then you should be able to construct a 3-body solution to Special Relativity in an algorithm. Of course you can just assume that it must all add up. But before you do that, first consider the following example. Next
we evaluate the formula for time-dilation according to Special
Relativity: |
||
|
(Formula simplified from Ohanian, p. 439) Because we divide by a
number less than 1 the new time ‘T’ is going to be a
higher number than the Newtonian time: ‘t’. But because
the faster object records less time, the new time ‘T’,
can only be the time of the external observer. (Feynman, p. 78.
Twin’s Paradox).
Let
us apply this formula such that, we consider a starting reference
point of zero velocity to be a satellite at the midpoint between
a binary pair of stars (or planets) in a circular orbit. This
pair then orbits one another at equal but opposite velocities
according to Newton: |
||
|
So in Special Relativity time is said to slow down when an object
approaches the velocity of light. Using the formula previously,
more time passes externally to the object that has greater velocity.
We are now going to get three different time situations depending on which starting reference point we use. If we take the satellite at the center of the pair as the zero-velocity reference – then time at the each of the binary pair would run slower than at the satellite – but time for the binary pair are equal to each other – in this instance. And yet, if we take either one of the stars as having zero velocity, then time at the other star has time running slowest because that star is moving fastest. So if we allow three clocks to exist in the three positions for a while, and then bring them together, which clock will empirically record the most advanced time? Well, it makes intuitive sense to take the barycenter as the zero-velocity reference point so that we can observe the shape of the binary orbit most clearly – so in the computer algorithm, the barycenter is always taken as the reference point. If we do this, then we reach the conclusion that both the stars have the same measurement of time according to Special Relativity. But if we consider any one star as the zero starting reference, then the other has velocity and vice versa. Thus they have velocity differences relative to one another, so they should therefore be suffering from contradictory time-dilation relative to one another! So Relativity gives us contrary consequences depending on the reference frame. And it does this because it tries to apply its formulae identically across any reference frame. It may also be theorized, that in a circular orbit, the distance between a pair is always constant so they would then have zero time dilation difference because they have a relative velocity of zero. But if they have zero velocity between them then gravity should pull them together. Of course that is wrong because the gravity is what is keeping them at an equal distance apart due to their mutual binary orbital movements. But that mutual orbit is only a meaningful concept relative to the midpoint as the starting reference. They require an objectively real orbital velocity when compared to one another to overcome gravity. Thus we have to conclude that their velocity relative to one another is meaningless as a starting reference. Only the midpoint as a starting reference will enable the pair to maintain a binary orbit. If we start with any one of the bodies having zero velocity then it will immediately acquire non-zero velocity caused by gravity from the other body. And this is just as true in Relativity as it is in the Newtonian paradigm. So it is essential to realize, that even a binary orbit is not actually a two-body system, because the barycenter is a third essential positional point. All binary orbits can only be properly calculated as a three-body system even if the third ‘body’ has no mass or gravity of its own. The midpoint (barycenter) is an essential objective positional aspect of any binary system. The orbit of the binary pair is only meaningful when observed to be moving compared to the objective notion of ‘fixed’ stars. The barycenter and the ‘fixed’ stars thus represent the same reference frame; without which any lack of movement between the pair will result in gravity starting to move the pair together – because they would then have no binary orbital structure. We
have already seen how it is impossible to objectively measure
time-dilation from Special Relativity. Now the Relativists claim
that this does not disprove Special Relativity, but instead they
claim that it proves that ‘simultaneity breaks down’.
They are thus claiming that the laws of physics give different
results depending on the reference frame – at the same time
they also claim that the laws of physics are the same in all reference
frames. |
||
| This is an extract summary of Chapter XXX of the book: Flight Light and Spin Download page for relativity simulation: algorithm orbit-gravity-sim-12.exe The full chapter can be downloaded here: Sum-Theory.pdf (5.5 mb, 57 pages, this pdf file is too big for chrome, use firefox) List of: abbreviated short articles . . |
|||||