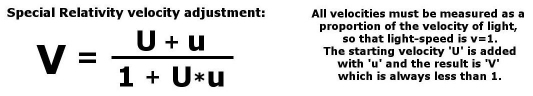| Relativity and the orbit of Mars The orbit of Mars in the algorithm orbit-gravity-sim-12.exe firstly shows how the velocity adjustment from Special Relativity alters the orbit of Mars. The orbit of Mars here also demonstrates how the polygon error-margin occurs in Newtonian gravity (in conjunction with quantum time). I am suggesting that because this orbit almost fits exactly into an equal number of sides in the orbit-polygon, a process occurs by which the data reveals that for 14 orbits, the orbit becomes increasingly eccentric, and then turns around and becomes more circular for 28 orbits. Theoretically the orbit should oscillate like this indefinitely, maintaining an average distance from the Sun throughout. (See Scenario [16] running at a time-ratio of 1:1 million). So
for the first 14 orbits, the maximum increases while the minimum
decreases, after which they switch around. So after 28 orbits, they
are almost back where they started. This is explained in more detail
in Section 27 (Using OGS12). Here is some
detail from Scenario [16]: |
||
|
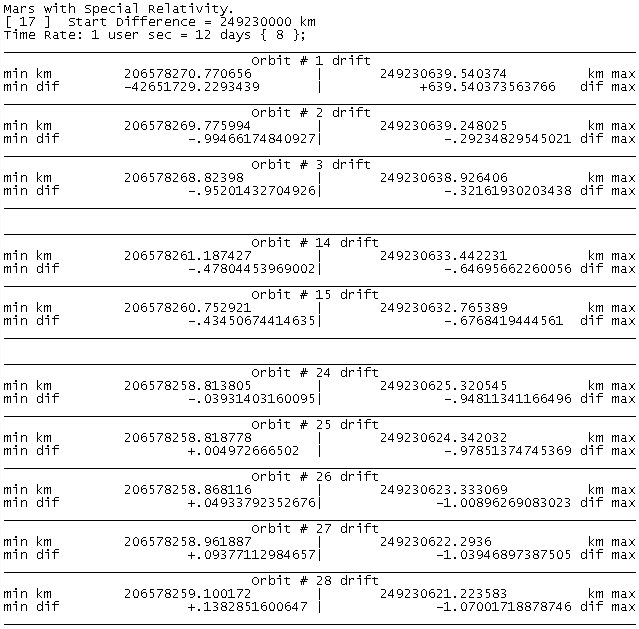
Pay special attention to the parts highlighted in red, which represents
the maximum distance from the Sun which Mars has fluctuated after
the 28th orbit: about 67 meters. This is an average of just 2.5m per
orbit over the 27 orbits. However, for the individual orbit #3 the
distance from Mars to the Sun fluctuates by 380 meters. (Ignore the
orbit #1 differences as they have no previous orbit to differ from,
and just reflect the difference from the start).
Can
you see how the orbit will become more eccentric due to the quantum
nature of orbital polygons from orbit #1 to orbit #14? And then
from orbit #15 onwards, they now become less eccentric. But the
key concept is that this effect is simply a coincidental error caused
by the computer algorithm. If the time-rate is changed so that the
software generates an orbit with a different number of sides to
the polygon, then the phenomenon simply disappears. If you want
the full data of all the orbits, you can generate it in the software
yourself. |
||
|
As can be seen, the orbit of Mars is also fairly eccentric so it
reflects a significant adjustment due to Special Relativity. The
total outward drift from the polygon error does not switch around
at orbit#14 and orbit#15 like it does under Newton (Scenario [16]).
Instead by orbit #28, Mars is 18km closer to the Sun. This is about 2/3rd of a kilometre per orbit on average that Mars would be moving towards the Earth’s orbit – if the limit at the velocity of light from Special Relativity causes a decrease in expected velocity. With
Mars being 54 mkm away from the Earth, and the effect of Special
Relativity on the orbit of the Earth being an inwards spiral of
only about 100m per year, we can expect Mars to collide with the
Earth in about 60 million years – but if and only if –
Einstein’s theory of Special Relativity is correct. The
effect of Special Relativity on the orbit of the Earth being about
100m per orbit is much less than it is on Mars because the Earth’s
orbit is less eccentric than Mars’ orbit is. |
||
|
Special Relativity also claims that this loss in energy has to
be compensated with an increase in the mass of the object –
in order to preserve the conservation of energy principle. Moreover
Feynman concludes that if the added velocity in the formula above
‘u’ is negative, then the formula is not reversible.
So for him ‘u’ must be a positive number. No mass
is lost or velocity gained if the object decreases away from light-speed.
On
p.88 of Six Not-so-easy-pieces, Feynman discusses how two objects
collide under the principles of Special Relativity: |
||
 |
||
| Now Miles Mathis disagrees with Feynman on this point. For Mathis, ‘u’ can actually contain a negative number. This would mean that Mars will not be colliding with Earth in 60 million years time. Mathis’ evaluation of Special Relativity§ is wholly more acceptable – because the time-frames computed by OGS12 (using Feynman’s interpretation) are going to result in the Earth’s orbit being about 30 million kilometres further from the Sun 300 million years ago. If this were true then the dinosaurs would have been living in an extremely frigid ice-age. So
Mathis can not only ‘save’ the Earth from a horrible
collision with Mars, but he could also save some face for the
Relativists. It is vital to see that Mathis’ interpretation
is not the standard one. Note how the standard concept specifically
considers an ‘approach’ to the velocity of light,
and not a decrease away from the velocity of light. |
||
| This is an extract summary of Chapter XXX of the book: Flight Light and Spin Download page for relativity simulation: algorithm orbit-gravity-sim-12.exe The full chapter can be downloaded here: Sum-Theory.pdf (5.5 mb, 57 pages, this pdf file is too big for chrome, use firefox) List of: abbreviated short articles . . |
|||||