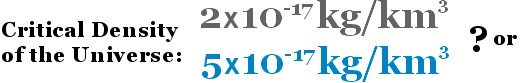| Critical Density of the Universe There
are several reasons as to why I claim that the popular concept of
a Critical Density to the Universe is simply wrong. This is quite
distinct from the assessment as to the actual density of the Universe
itself, and also different as to how the Critical Density is calculated. |
||
|
#1: The most obvious
misunderstanding of the Critical Density is that at some earlier time,
the actual density of the Universe is going to be more than the Critical
Density of the Universe, regardless of the amounts concerned. Many
claims are made that the Universe is currently at that Critical Density.
So how could the Universe have expanded to the current density from
a state that was denser – if that more dense state would have
made it impossible for expansion to occur?
#2: The role of orbital structures has simply been ignored. The concept of Critical Density typically hinges on radial attraction between bodies. If two masses are in an orbital structure, they will not pull together into a single entity; they will orbit one another indefinitely. Previously I examined the role that the various theories of Relativity play in this. But regardless of that, the actual mathematical process by which Critical Density is arrived at simply ignores all orbital structures completely. This type of error occurs because of fixation on regurgitating math in scholastic ‘exams’, rather than individuals wilfully and freely constructing observable computer algorithms themselves – which requires a wider scope for the imagination to contextualize the math into a single over-arching logical structure. If the motive for study is personal it is authentic. The alternative is academic toadying. #3: In the previous section the concept of Local Galaxy Density was introduced. If we distribute the mass of the Milky-way over a volume of space extending to the nearest major galaxy then the density of the local region of the Universe is 7.5x10^-16kg/km^3. So if Critical Density prevents expansion, then the local galaxies should have contracted into a single entity a long time ago. #4: The density of our solar system itself is far more than the Critical Density of the Universe. But because our solar system has orbital structure – the planets do not simply collapse into the Sun. Instead the planets orbit the Sun. #5: A 4d-structure makes Critical Density unworkable. Consider the balloon analogy with gravity attracting only along the surface. Because all objects attract all other objects, every pull in one direction is counter-acted by a pull in another direction. Critical Density hinges on the notion of escape velocity. Escape velocity implies that there is empty space that the object can escape towards. Objects in a Universe that wraps around have no space to escape into. So escape velocity for the whole Universe is meaningless if we have a closed Universe. #6: Even if we ignore the previous arguments, and simply look at how long it takes for bodies at the Critical Density to coalesce under gravity, the amount of time is higher than the age of the Universe. So regardless of theoretical context and philosophical reasoning, their sums are just plain wrong anyway. So we let us examine how long it takes for 1kg of matter at the ‘Critical Density’ to coalesce when dispersed over space. To
do this we invert the Critical Density and then cube root that volume: |
||
|
The two objects of 1kg each must be placed about 370 thousand kilometres
apart according to popular astrophysics to counter the expansion
of the Universe, whereas in Sum Theory they need to be just 270
thousand km apart. These distributions in linear space thus represent
the claims to Critical Density. Then we apply gravity and we wait
and see if it takes the age of the Universe for them to pull together.
There is a beautiful and neat feature of how gravity and density interact that needs to be elucidated. Scenario [31] and Scenario [32] of the OGS12 algorithm (orbit-gravity-sim-12.exe) both represent the Critical Density according to Sum Theory. However in Scenario [31] it is a pair of 1kg objects 272 400 km apart, whereas in Scenario [32] the pair of objects are 1000kg at a distance apart of 2.724 million km. They both give the required time of about 13.7 billion years to attract. The amazing thing is that when the density is the same, the time it takes them to attract together is also the same. The actual volume and mass make no difference to the time it takes for them to attract together. So long as the volume and mass are at the same proportion, the time to coalesce is identical. I am uncertain if anyone has noticed this before, so I’ll just call it the Beautiful Attraction Principle. So when I place the popular astrophysics amount of Critical Density into Scenario [33], I am really just being thorough. I do this because the way in which popular ‘Critical Density’ has been calculated seems to ignore how easy it is to actually determine what it should be. Certainly, all the other ways for determining Critical Density seem to suggest that it is important to know the volume and mass of the entire Universe. All that is actually required is the age of the Universe and a simple calculation. But, of course Critical Density is actually a failed concept for reasons #1 to #5 outlined earlier. Nevertheless, when we take the Critical Density of popular astrophysics to be 2x10^-17 kg/km^3 (or 2x10^-26 kg/m^3) we get the result that it will take the pair of 1 kg objects at 370 thousand km apart an enormous 21 billion years to completely attract one another. And it is this feature I have called the Beautiful Attraction Principle that makes everything so much easier. Because it does not matter how much space and mass we are dealing with. Regardless of whether it is 1 kilogram, 1 ton, or all the mass in the Universe – if the density is the same, the time it takes to coalesce is identical! But of course, this is only true for horizontal linear movements and does not at all take into account: orbital structures or collisions. A small amount of contrary velocities vertically, leaves them in an orbit that never contacts one another! So the time to coalesce here is a minimum time. The real time will always be more than this anyhow. Next we have to consider the rate of expansion too. The OGS12 algorithm and the ordinary formulae (in the section to follow) only compute a static un-expanding Universe. But if we consider that some expansion in the past counterbalances some expansion in the future, we still get the Critical Density for now. So
in the next section let us double-check all these results using
conventional formulae: |
||
| This is an extract summary of Chapter XXX of the book: Flight Light and Spin Download page for relativity simulation: algorithm orbit-gravity-sim-12.exe The full chapter can be downloaded here: Sum-Theory.pdf (5.5 mb, 57 pages, this pdf file is too big for chrome, use firefox) List of: abbreviated short articles . . |
|||||