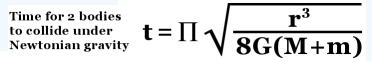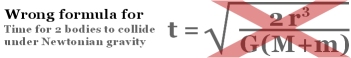So how do we decide what is the correct formula? Well the OGS12 algorithm uses the most ordinary equations for gravity (g=m/r^2) then simply allows time to compute in a purely evolutionary manner – and this program gives excellent results to within a matter of millimetres for the orbits of the Moon, the Earth and other planets – even when not running at its most precise rate of computation.

So if we consider the data from the previous section, and place it into the correct exact formula so that we can establish:

{A} How long it will take for gravity to attract a pair of 1kg objects if they are:
272 400 km apart – the answer is 13.7 billion years.

{B} How long it will take for gravity to attract a pair of 1kg objects if they are:
368 400 km apart – the answer is over 21 billion years.

Now for {A} the mass-per-volume is 1kg per 2x10^16 km^3,
and for {B} the mass-per-volume is 1kg per 5x10^16 km^3.

So if we invert those amounts we see that the volume-per-mass is then:
{A} 5x10^-17 kg/km^3
{B} 2x10^-17 kg/km^3

Be careful of the detail in those last two conversions. When we are converting the amounts from mass-per-volume to volume-per-mass we should do this one step at a time like this:
.

So because we have determined the Universe is 13.7 billion years old, the critical density can only be 5x10^-17 kg/km^3 {A}, whereas {B} yields a density that will coalesce in a much longer time than the age of the Universe.

Another amusing example we can use is two 75g objects 10cm apart. They would take about 3 hours to attract together due to gravity. Now the Beautiful Attraction Principle (see previous section) shows us that if two objects, one of 100kg, another of 50kg, are 1 meter apart, then under gravitational attraction it would also take about 3 hours for them to make contact. This is the same for two 75kg objects 1 meter apart. Or, an object at 85kg and another at 65kg at 1 meter would yield an identical result.

Beautiful Attraction Principle:
The time it takes to attract is the same because the density in all these examples is identical.
.